一、K近邻算法介绍

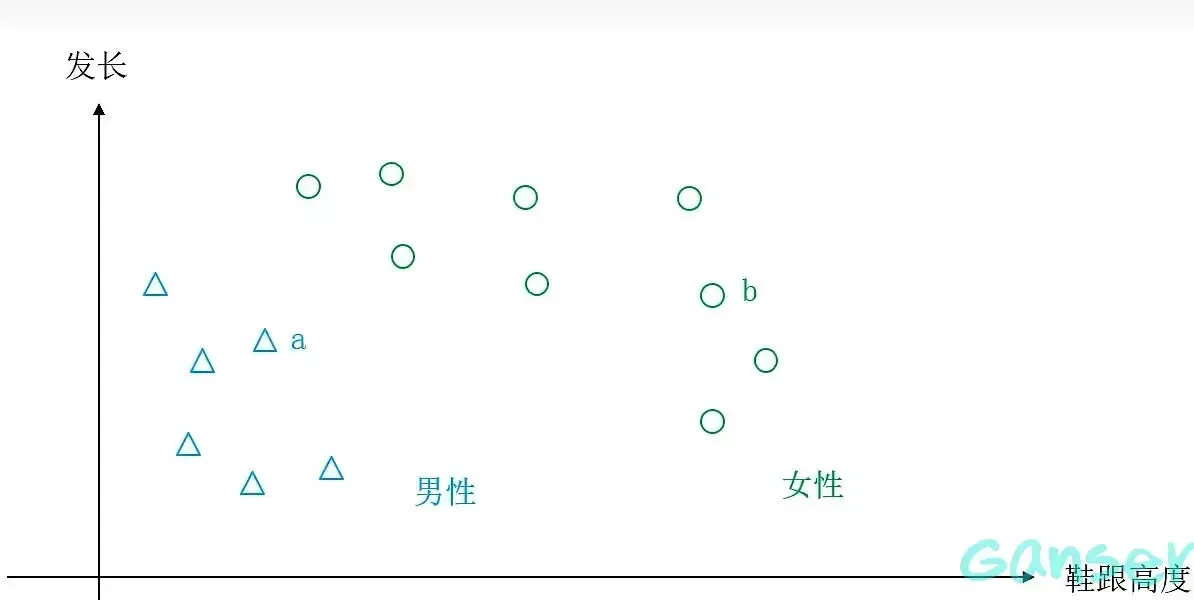
K近邻是一种不需要训练的分类方法，其基本思想为物以类聚，相近的样本属于同一类别的概率大。

假设待分类样本$x$距离已知样本$a$的距离最近，我们认同待分类样本$x$与已知样本$a$属同一类（男性）。反之，若距离已知样本$b$距离最近则认同待分类样本$x$与$b$同类为女性。（以上均为最近邻）。

二、K近邻方法

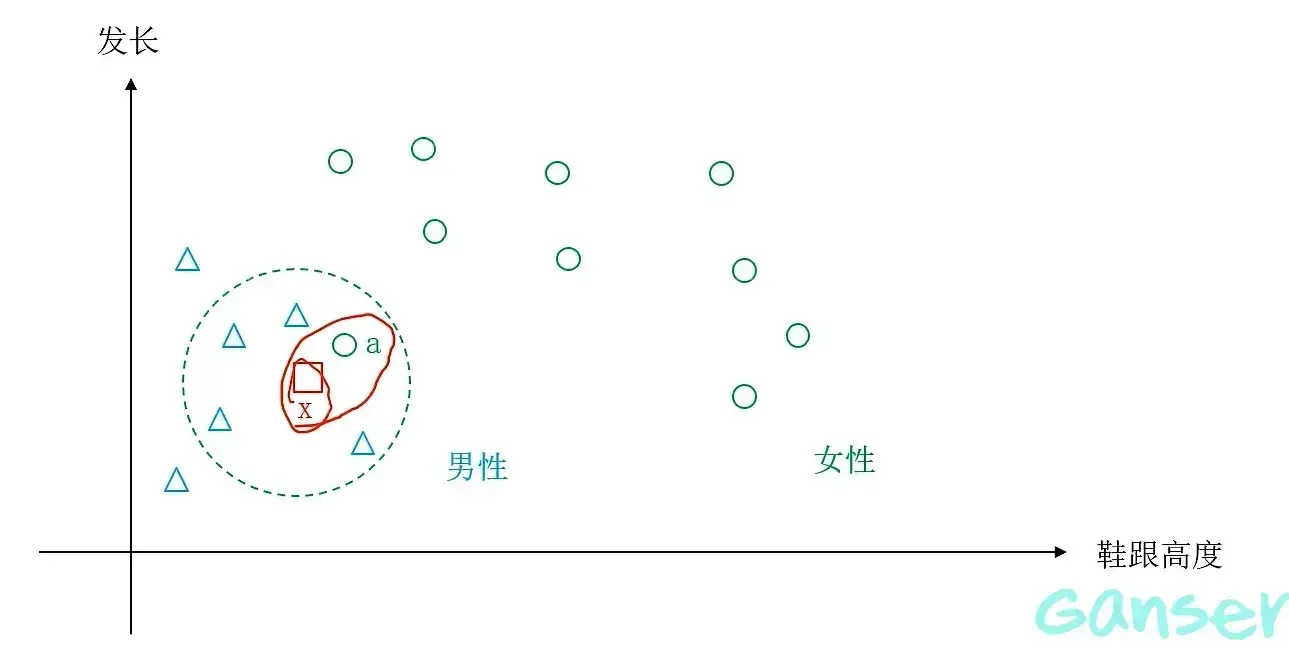
以上最近邻方法存在一些疑问，当数据样本存在噪声时（假设样本标签存在标记错误）或有一些样本虽被标记为男性（女性）但不具备对应性别的典型特征，这样依据最近邻对待分类样本进行分类，为免存在武断，误判等问题。因此，为了解决这一问题，我们需要将视野扩大到待分类样本周围k个样本。这种方法就是K近邻算法

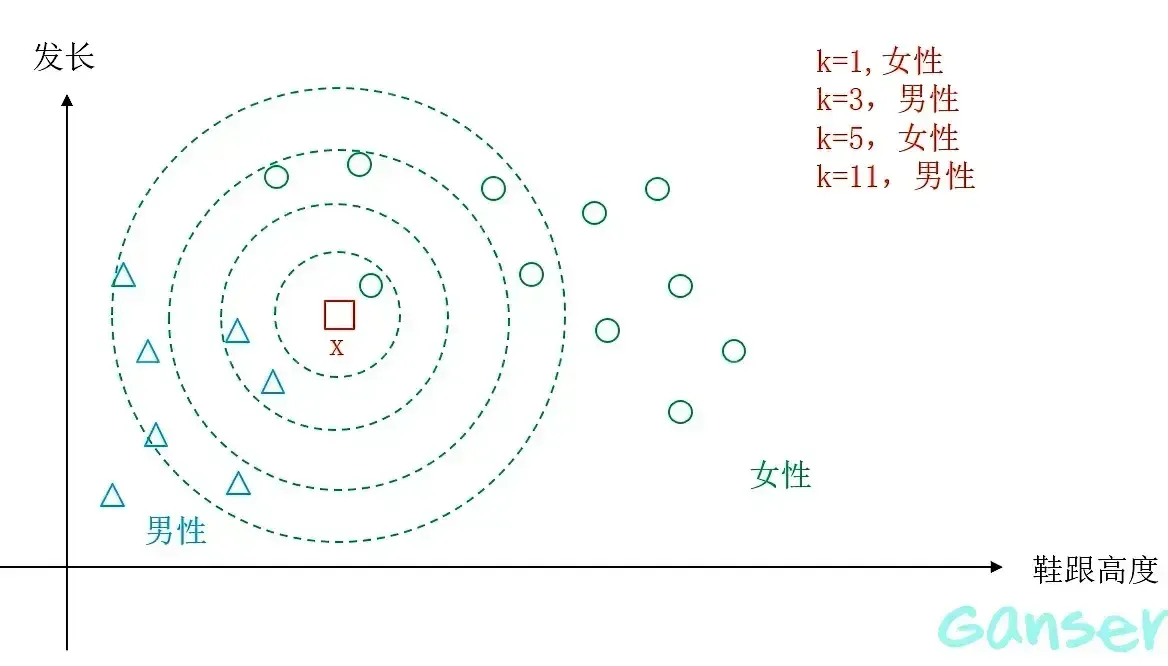
2.1 K值的影响

K近邻算法中若K取1，则为最近邻算法，K值的合适取值，决定着该算法的精度。K值的选择很难有一个定量的方法，基本上就是做实验。

2.2 距离计算

距离计算有很多种，这里介绍三种典型的距离计算方法。

2.2.1 欧氏距离

欧式距离实际上就是直线距离：

2.2.2 加权欧式距离

方差的倒数做加权：$a_k=\frac{1}{S_k}$，避免部分均方结果影响大：

$$
L_2(x_i,x_j)=\sqrt