一、过拟合问题

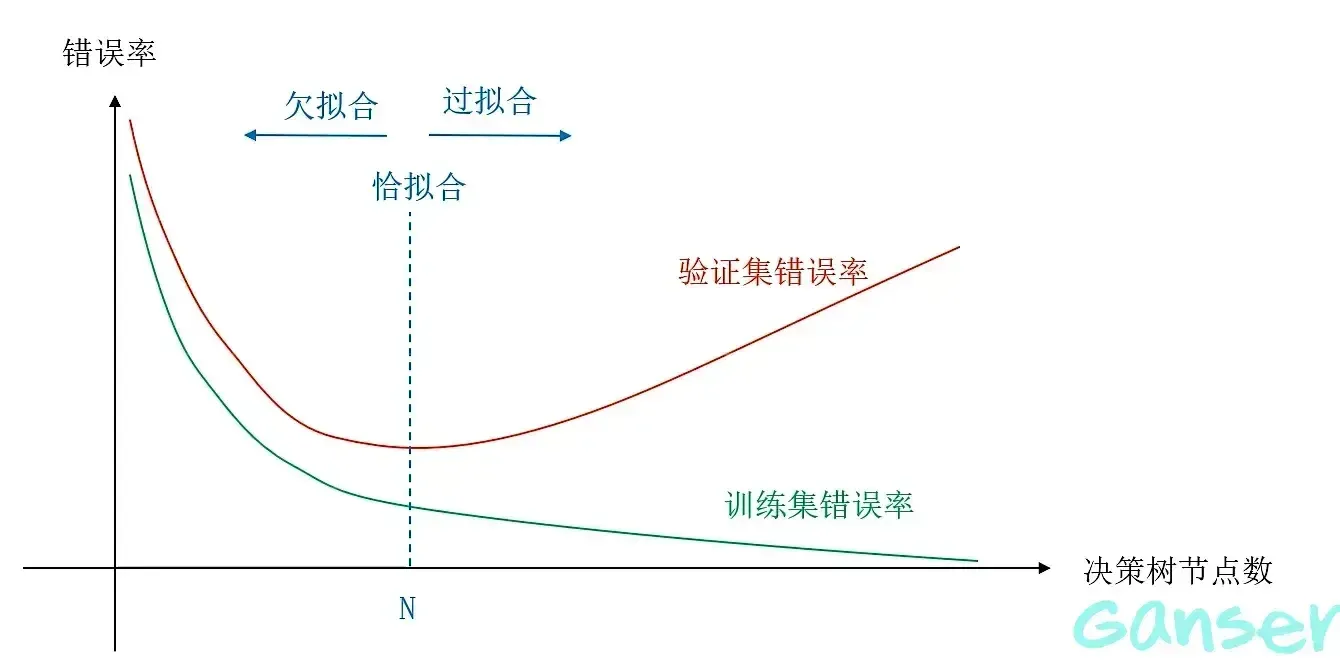
我们将一个数据集划分为三个子数据集：训练集、验证集、测试集。过拟合现象，即：随着决策树节点数的增多，训练集的错误率逐渐减小，但验证集错误率呈先减小后增大的趋势。

因此在建立决策树时，我们需要寻找恰拟合的决策树，这样避免过拟合现象同时达到验证集错误率最小，故引入剪枝方法。

二、剪枝方法

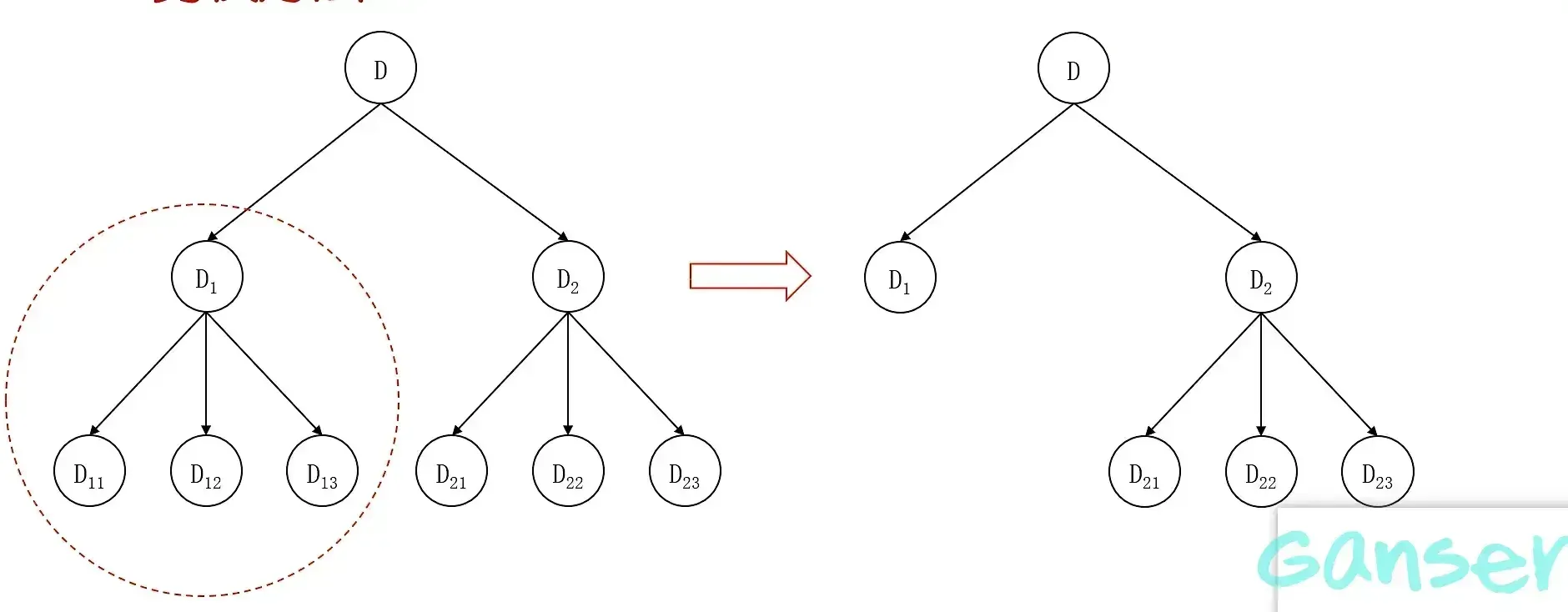
决策树中的剪枝方法，即减少树中结点的个数。剪枝方法的基本思想为：剪枝前后，决策树在验证集的错误率减少，是一种自下而上的减少结点数量方法。

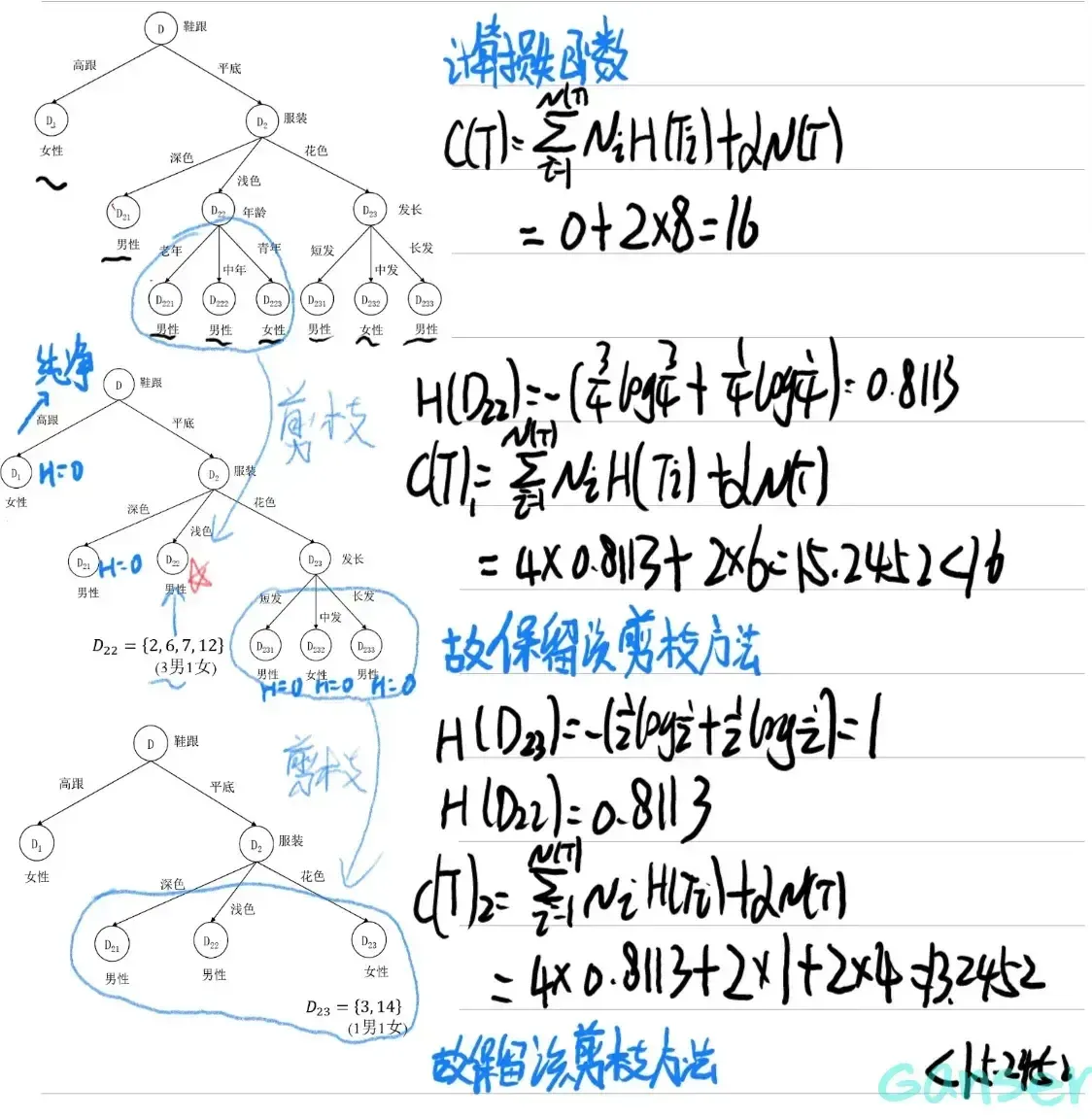
以上方法进行剪枝，未免过于麻烦，因此引入损失函数方法进行剪枝，它是通过综合考虑决策树的大小和训练集上的错误率来影响剪枝过程。

三、损失函数

其中，$N(T)$表示树T的叶节点树，反映了决策树的大小。$H(T_i)$表示叶节点$T_i$的熵，反映了训练集的错误率。$N_i$表示叶节点$T_i$的样本数。$\alpha$表示调节系数。