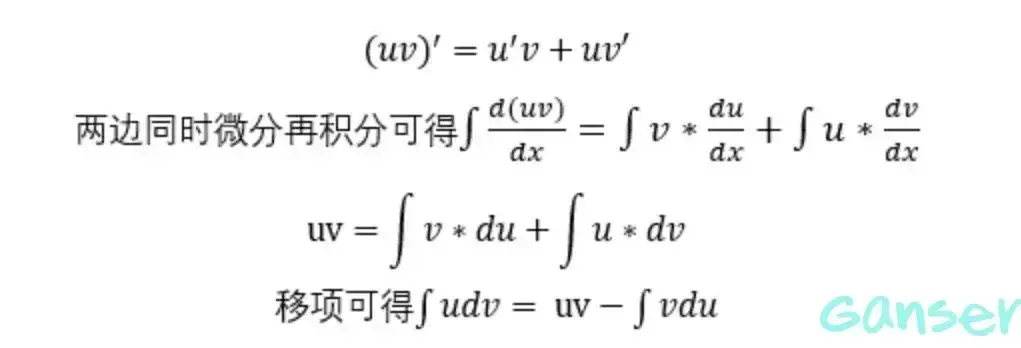最近需要求积分的地方越来越多了，比如数学物理方程和信号与系统。天下苦微积分久矣，因此想找一些简单的方法进行求解，就看中了由分部积分法延申出的表格法。这是张宇老师所讲的一种方法。

一、分部积分法

要介绍的表格法是由分部积分法延申而来，那么我就浅浅的提一下分部积分法。

分部积分法是微积分学中的一类重要的、基本的计算积分的方法。它是由微分的乘法法则和微积分基本定理推导而来的。它的主要原理是将不易直接求结果的积分形式，转化为等价的易求出结果的积分形式的。常用的分部积分的根据组成被积函数的基本函数类型，将分部积分的顺序整理为口诀：反对幂指三。分别代指五类基本函数：反三角函数、对数函数、幂函数、指数函数、三角函数的积分。

上述表明在出现以下两种情况下我们选择分部积分法进行积分求解：① 出现了不同类型函数乘积的时候；② 求$\int{u}dv$复杂但是$\int{v}du$简单；

其公式推导如下

反对幂指三也是分部积分法选取$u、v$的口诀，大家高数都学过，这里不做介绍。

二、表格法

利用以上推导出的分部积分法的结果$\int{u}dv = uv - \int{v}du$，推导表格法

借此得出计算方法：以$u$作起点左上、右下错位相乘，各项符号+、-相间，最后一项为$(-1)^{n+1}\int{u^{n+1} v}dx$

网友总结：交叉相乘，起点为正，正负相间，最后+C

那么求导的$u$函数什么时候可以停止呢？

我也不清楚，看总结的大抵上都是说求导为0时、像$cos,sin,e^x$这样求导会重复的项重复了就不要求了，求导变复杂了也不要求了，就是这样。

三、例题