可变形卷积是相对于标准卷积来说的，这个概念出自于Hu han团队在2017年发表的一篇论文《Deformable Convolutional Networks》。既然该概念是相对于标准卷积来说的，那么我们就有必要将两种卷积进行对比学习。

一、标准卷积

首先，对于标准卷积我们可以借用下面的数学表达式理解：

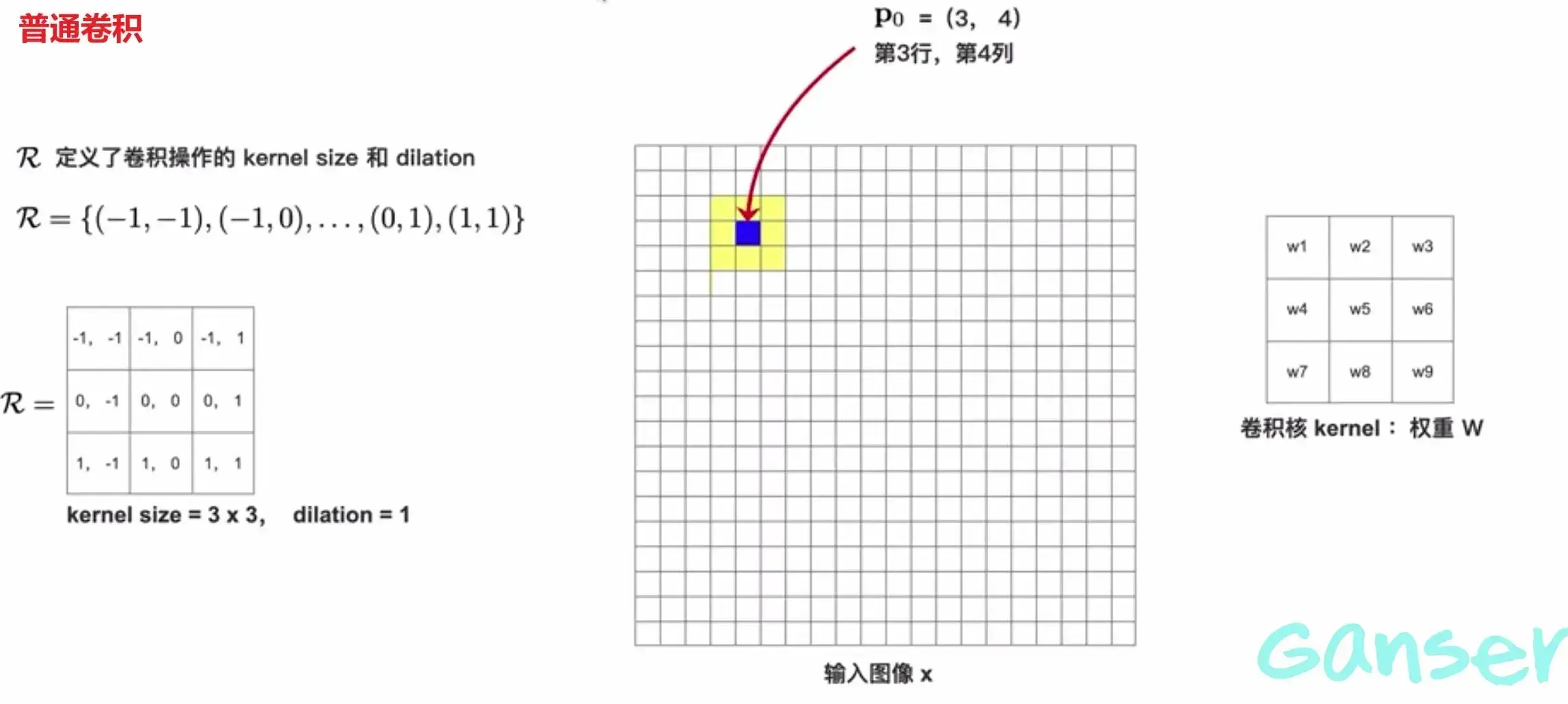
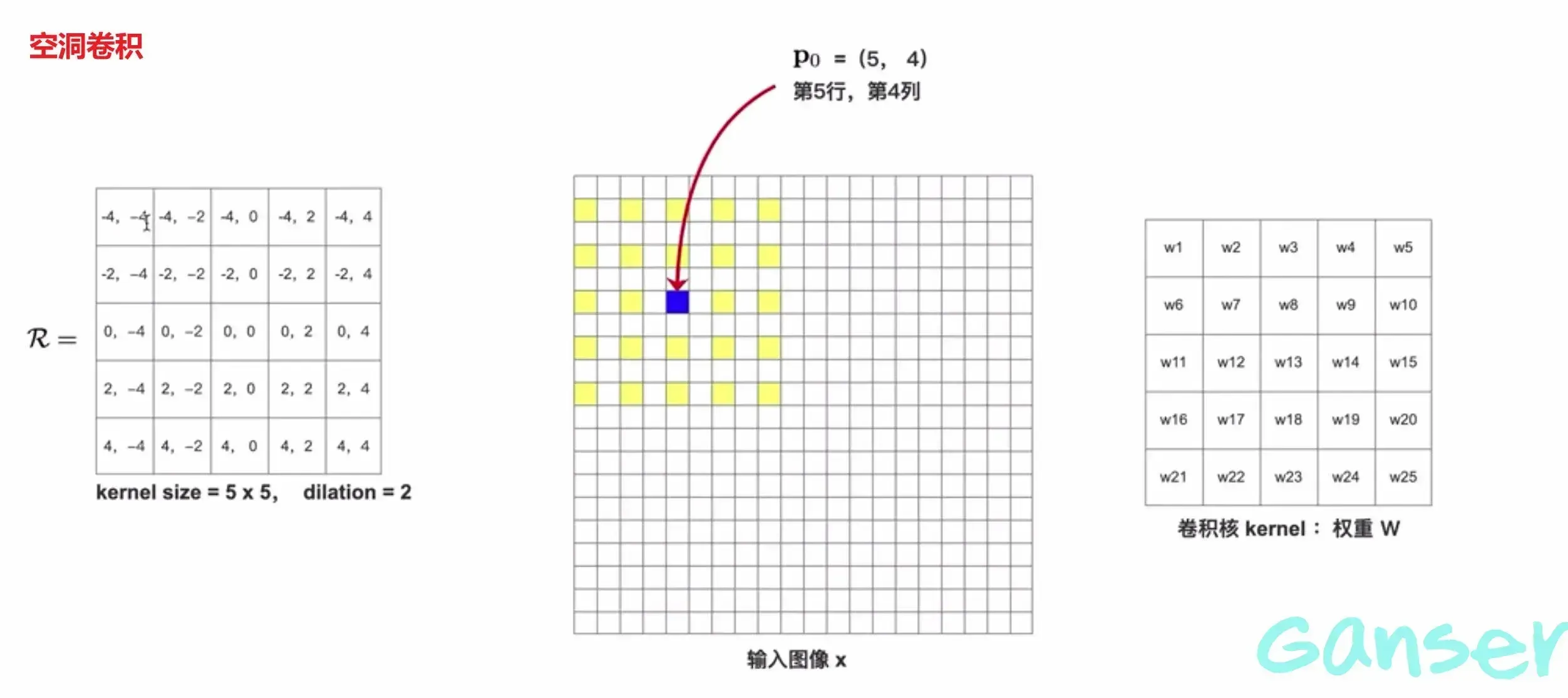
这里$p_0$代表中心像素的坐标，$p_n$代表基于窗中的临近元素坐标，它是相对于$p_0$的，$x(·)$代表像素的像素值，$w(p_n)$代表卷积权重，$R$是由$p_n$与$p_0$共同构成相对位置坐标的矩阵/集合。在这里$R$定义了卷积尺寸和卷积模式（空洞卷积或者普通卷积）。

卷积的运算，即相乘相加，将尺寸为3x3的感受野中的信息通过卷积的运算聚合到map中的一点。

二、可变形卷积

对于可变形卷积我们可以借用下面的数学表达式理解：

注意到可变形卷积是在标准卷积的基础上加上了位置偏移量offset$(▲p_n)$，在论文中指出$▲p_n$是学习得到的值，为小数，由图像经过普通卷积计算得到，下面理解该$▲p_n$是如何得到的。

2.1 Offset计算得到

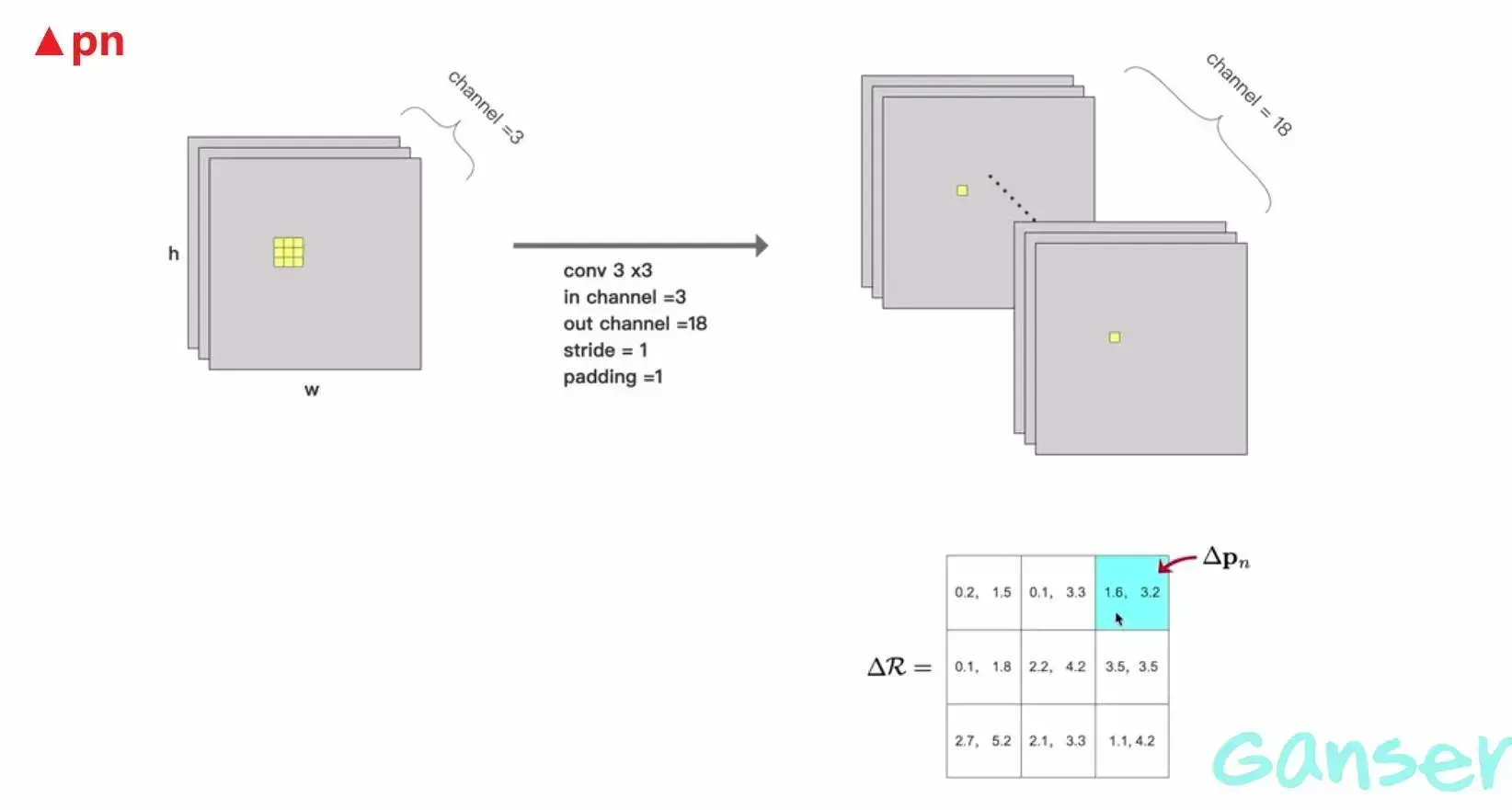
上面指出offset是有普通卷积得到，对于普通卷积的卷积核设置做如下规定：

• in_channel等于输入图像的channel_num
• out_channel等于二倍的kernel_size的平方(这里的kernel_size为可变形卷积的kenel_size)
• stride，padding均有$p_0$决定

在下图中得到channel等于18的feature map后我们将由尺寸为3x3的感受野经过卷积得到的抽象信息（拥有18个channel）拿出来做reshape得到$▲p_n$

2.2 可变形卷积的操作过程

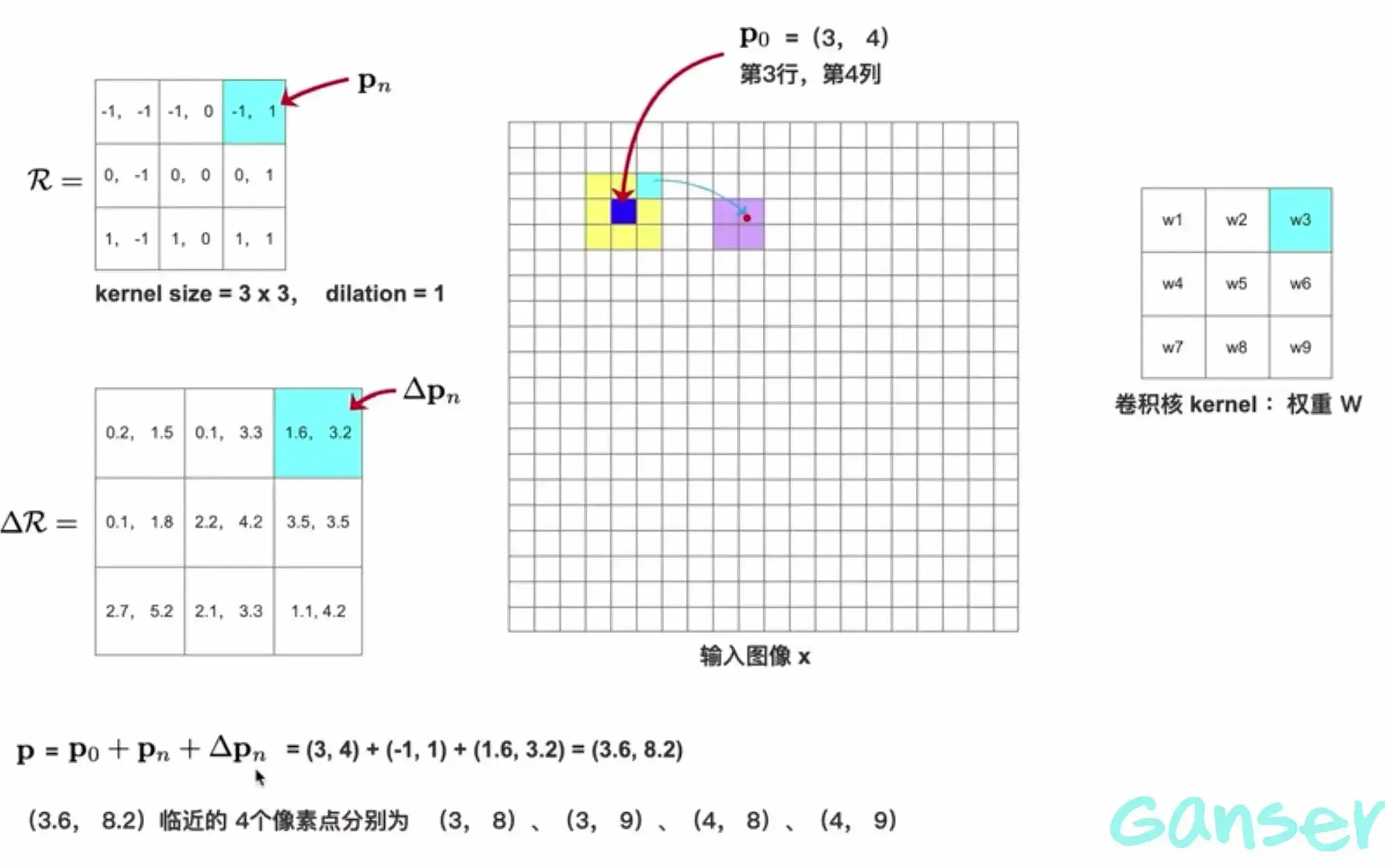
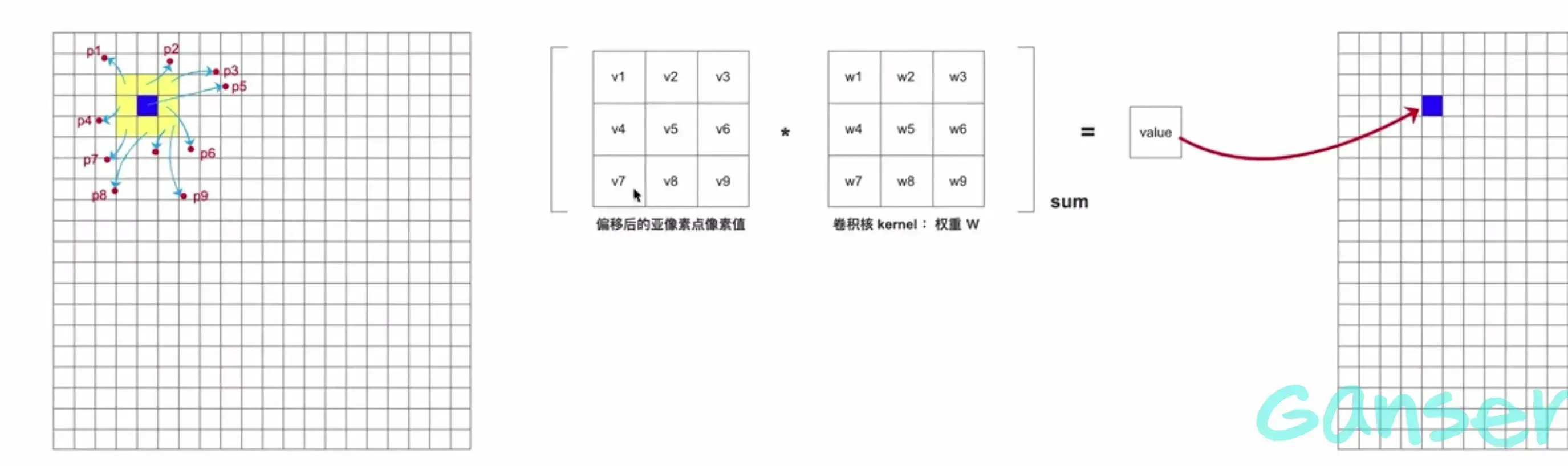
针对以上得到的$▲R$偏移位移矩阵，用于计算$p_0$相邻元素的偏移位置，从而得到偏移后的像素值（称之为亚像素点的像素值），使用该像素值与卷积核进行卷积从而得到可变形卷积的结果。

这样可变形卷积的操作就此完成。作者在针对偏移坐标的像素值的求解使用双线性插值法求得。找到亚像素点相邻的4个像素点，用该方法求解目标亚像素点的值。

本内容引用B站Enzo_Mi大佬的视频内容。